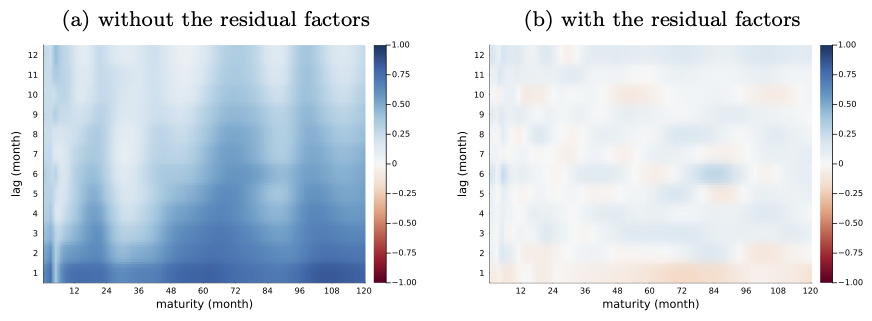
Figure 1. Autocorrelation in the residuals. The figure illustrates the autocorrelation of the residuals from the regression of bond yields. Panel (a) shows the results when using the first three principal components of bond yields as regressors, while panel (b) presents the results when both the principal components and the residual factors are used as regressors.

One concern that arises when analyzing bond market models is the strong autocorrelation hidden in the pricing errors of the estimated models. This suggests the presence of systematic movements that traditional bond market models fail to capture. The most rigorous solution is to refine theoretical models to whiten these pricing errors. However, given that traditional models explain nearly 100% of the cross-sectional variation, the practical significance of the remaining autocorrelation in residuals may be negligible. If that is the case, the necessity of improving theoretical models diminishes. In my new study, I examine whether the residual autocorrelation contains additional predictive power and whether leveraging it can enhance bond investment returns.

To this end, I construct seven factors called “the residual factors” and examine its additional predictive power. The left panel of the figure illustrates the autocorrelation in pricing errors when fitting the yield curve using only the traditional first three principal components of the yield curve. In contrast, the right panel presents the autocorrelation in pricing errors when the residual factors are additionally incorporated. As shown in the figure, the residual factors effectively capture the autocorrelation in residuals. The theoretical foundation of the residual factors can be found in Crump and Gospodinov (2022).

My findings indicate that the autocorrelation in residuals provides additional predictive power and enhances investment returns. However, its effectiveness declines somewhat after the 2008 financial crisis. Whether this downward trend will persist in the future remains uncertain. Additionally, incorporating residual autocorrelation into portfolio optimization leads to frequent rebalancing, resulting in significant transaction costs. Nevertheless, our paper suggests that the autocorrelation in residuals is difficult to ignore from a practical perspective. A theoretical model that accounts for this autocorrelation appears necessary.

Finally, to explore the macroeconomic interpretation of the residual factors, I conduct a regression analysis using the residual factors as dependent variables and macroeconomic variables as regressors. The results show that both the traditional three principal components and the residual factors are significantly influenced by price and labor market variables. This suggests that the residual autocorrelation contains macroeconomic information similar to that embedded in the traditional three factors. However, less than 50% of the variation in the residual factors can be explained by macroeconomic variables, indicating that modeling these residual factors from a macroeconomic perspective may be challenging.